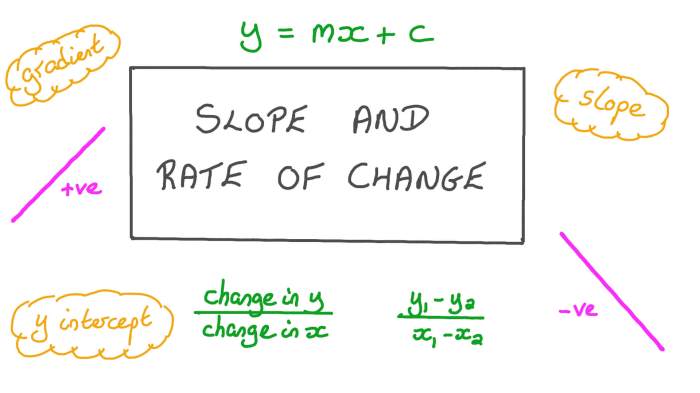Lesson 3-2 rate of change and slope – Embarking on Lesson 3-2: Rate of Change and Slope, we delve into a realm where quantities transform over time. Understanding this fundamental concept is paramount, as it quantifies how variables evolve, empowering us to analyze real-world phenomena and make informed predictions.

Delving deeper, we unravel the intricate relationship between the rate of change and slope, unveiling their significance in interpreting the behavior of functions. Through meticulous calculations and insightful examples, we illuminate the practical applications of these concepts, empowering learners to harness their knowledge in diverse fields.

Introduction to Rate of Change and Slope

In mathematics, rate of change and slope are two fundamental concepts used to describe how a quantity changes over time or in relation to another variable. Understanding these concepts is crucial in various fields, including science, economics, and engineering.

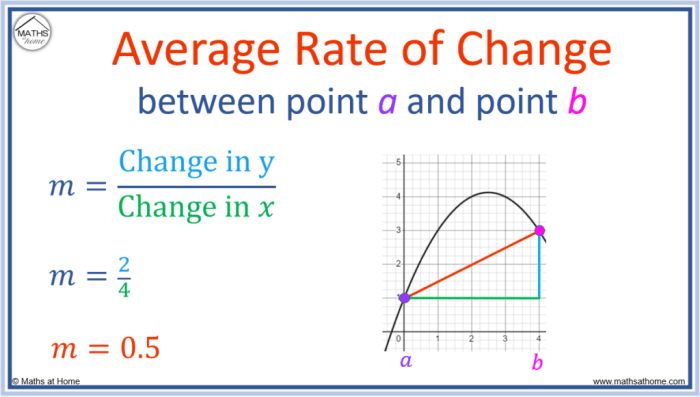
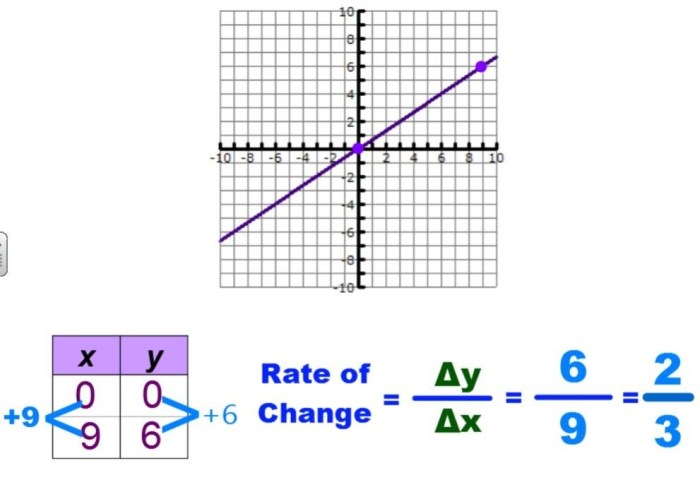
Rate of change measures the speed at which a quantity changes per unit of time or with respect to another variable. Slope, on the other hand, represents the ratio of the change in the dependent variable to the change in the independent variable in a linear relationship.

Calculating Rate of Change and Slope

The rate of change can be calculated using the following formula:

Rate of Change = (Change in Dependent Variable) / (Change in Independent Variable)

Similarly, the slope of a linear relationship can be calculated as:

Slope = (Change in Dependent Variable) / (Change in Independent Variable)

These values can be calculated using tables, graphs, or equations.

Interpreting Rate of Change and Slope

The sign and magnitude of the rate of change and slope provide valuable information:

• A positive rate of change indicates that the quantity is increasing.
• A negative rate of change indicates that the quantity is decreasing.
• A zero rate of change indicates that the quantity is constant.
• An undefined rate of change occurs when the change in the independent variable is zero.

Similarly, the slope of a line:

• A positive slope indicates a positive linear relationship.
• A negative slope indicates a negative linear relationship.
• A zero slope indicates a horizontal line.
• An undefined slope indicates a vertical line.

Applications of Rate of Change and Slope

Rate of change and slope have numerous real-world applications:

• In science, they are used to model and analyze physical phenomena, such as the speed of a falling object or the rate of chemical reactions.
• In economics, they are used to analyze market trends, such as the relationship between supply and demand or the growth rate of a company.
• In engineering, they are used to design and analyze structures, such as bridges and buildings, to ensure their stability and safety.

Advanced Concepts in Rate of Change and Slope, Lesson 3-2 rate of change and slope

In calculus, rate of change and slope are related to derivatives and integrals:

• The derivative of a function represents the instantaneous rate of change of the function at a given point.
• The integral of a function represents the total change in the function over a given interval.

These concepts are essential in advanced mathematics and have applications in fields such as physics, engineering, and economics.

Q&A: Lesson 3-2 Rate Of Change And Slope

What is the rate of change?

The rate of change measures how a quantity varies over time or with respect to another variable.

How is slope calculated?

Slope is calculated as the ratio of the change in the dependent variable to the change in the independent variable.

What is the significance of a positive rate of change?

A positive rate of change indicates that the dependent variable is increasing as the independent variable increases.